Probability | Conditional | Joint Poisson

Question

Suppose that the number of people who visit a yoga studio each day is a Poisson random variable with mean \(\lambda\). Suppose further that each person who visits is, independently, female with probability \(p\) or male with probability \(1−p\). Find the joint probability that exactly \(n\) women and m men visit the academy today.

Solution

Dissecting the problem. I will try giving a brief explanation of the solution here. For a high detail of the problem, please refer to the text. Notice that there a constraint on the sum itself but \(n\) and \(m\) themselves could be variables given that they add up-to a number. The probability that we need can be denoted as follows. \[P\{N_1=n, N_2=m\} = \overset{\infty}{\underset{i=0}{\Sigma}} P\{N_1=n, N_2=m | N = i\} P\{N=i\}\] where \( N = N_1 + N_2\). The probability that \(P\{N=i\}\) is a poisson distribution shown as \[e^{-\lambda} \frac{λ^{n+m}}{(n+m)!}\] Since there are two components to the poisson count, we need to introduce a binomial here and simplifying them we get two probabilities as \[P\{N_1=n\} = e^{-\lambda p} \frac{(\lambda p)^n}{n!}\] \[P\{N_2=m\} = e^{-\lambda q} \frac{(\lambda q)^m}{m!}\]

Reference: Sheldon Ross Probability Modelling Edition 10

Simulations

Approach to the simulations for this problem

Pick an arbitrary \(\lambda\) for the Poisson Random Variate. Here I have chosen \(\lambda = 5\)

The poisson outputs are numbers or the total number of people (male and female) visiting the yoga studio on a given day

Pass these numbers into a function that divides the number into males and females

For example, if the total number of people visiting the studio is 6, then this function would give the following combinations
- 0-Females & 6-Males
- 1-Females & 5-Males
- 2-Females & 4-Males
- 3-Females & 3-Males
- 4-Females & 2-Males
- 5-Females & 1-Males
- 6-Females & 0-Males

Then, we need to reformat the data to match the input format for the BarChart
All the above has been done in code that has been presented below the charts



    ClearAll[genderDivide]

    genderDivide[n_, p_: 0.5] :=
     Module[{genderDivide =
        RandomChoice[{p, 1 - p} -> {0, 1}, n]}, {Count[genderDivide, 0],
       Count[genderDivide, 1]}]

    Table[
     Module[{plot},
      plot = BarChart[
        Plus @@@
         GatherBy[
          genderDivide[#, p] & /@
           Sort@RandomVariate[PoissonDistribution[5], 10000],
          Total@# &],
        ChartLayout -> "Stacked",
        LabelingFunction -> (Placed[Rotate[#, 90 \[Degree]], Above] &),
        Frame -> True,
        PlotLabel -> Style["Probability for females = " <> ToString@p, 20],
        FrameLabel -> (Style[#, 15] & /@ {"Stacked Counts",
            "Total number of people"}),
        ImageSize -> 788, ChartLegends -> {"Female", "Male"}];
      Export[StringReplace[NotebookFileName[],
        ".nb" -> "_stacked_chart_" <> ToString[Round[10 p]] <> ".svg"],
       plot,
       ImageSize -> 1000, ImageResolution -> 800]
      ]
     , {p, 0.1, 0.9, 0.1}]

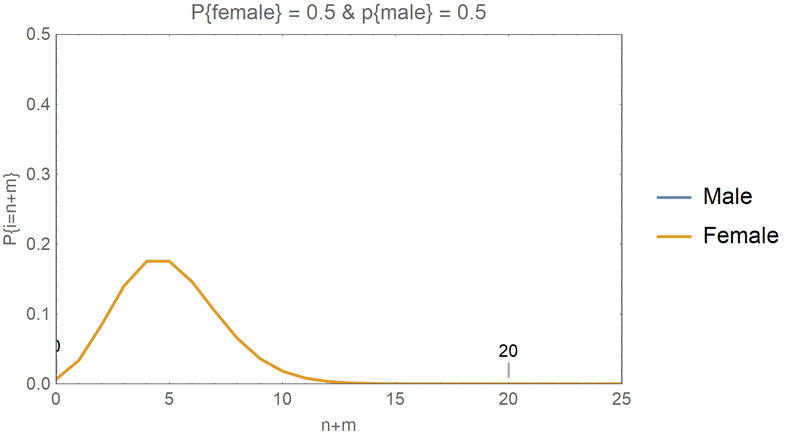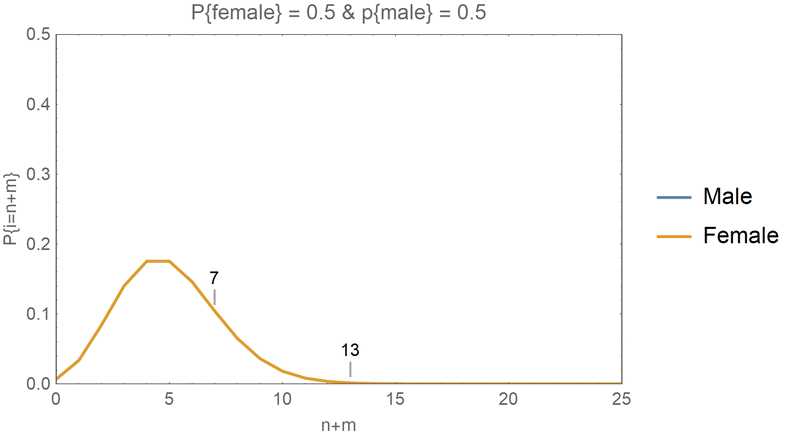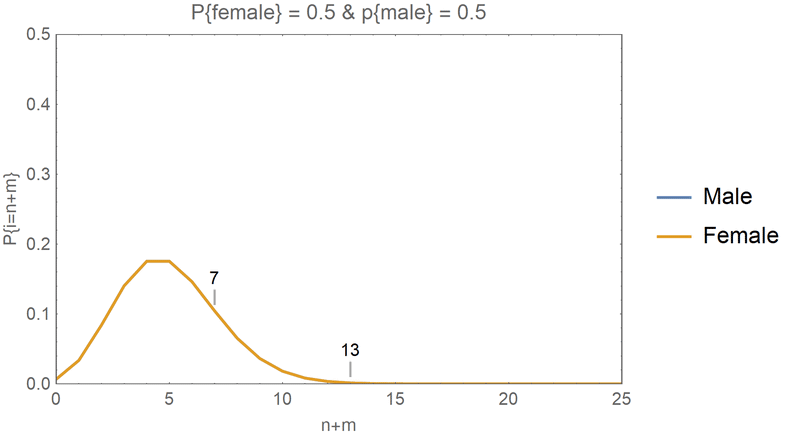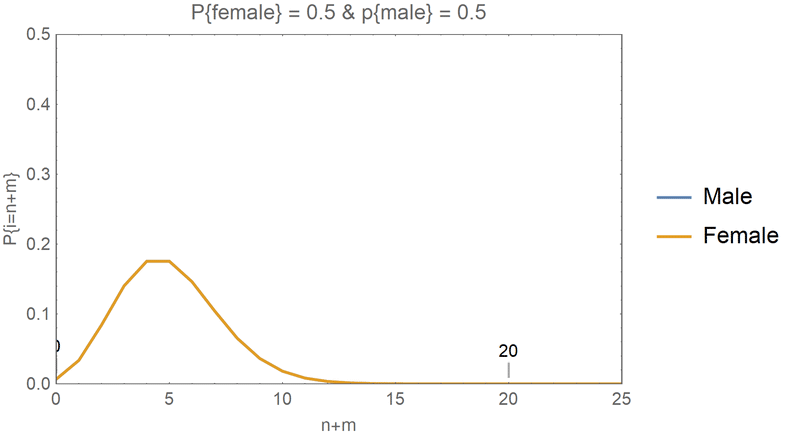
Theoretical Probabilities with Special Cases

In the animations that follow, I have fixed the \(\lambda\) to be 25.
Then, I have examined the cases where the total number of people is 20.
This means that the 20 people could be formed from any one of the following cases

\(N_{\text{females}} = 0 \text{ and } N_{\text{males}} = 20\)
\(N_{\text{females}} = 1 \text{ and } N_{\text{males}} = 19\)
\(N_{\text{females}} = 2 \text{ and } N_{\text{males}} = 18\)
\(N_{\text{females}} = 3 \text{ and } N_{\text{males}} = 17\)
\(N_{\text{females}} = 4 \text{ and } N_{\text{males}} = 16\)
\(N_{\text{females}} = 5 \text{ and } N_{\text{males}} = 15\)
\(N_{\text{females}} = 6 \text{ and } N_{\text{males}} = 14\)
\(N_{\text{females}} = 7 \text{ and } N_{\text{males}} = 13\)
\(N_{\text{females}} = 8 \text{ and } N_{\text{males}} = 12\)
\(N_{\text{females}} = 9 \text{ and } N_{\text{males}} = 11\)
\(N_{\text{females}} = 10 \text{ and } N_{\text{males}} = 10\)
\(N_{\text{females}} = 11 \text{ and } N_{\text{males}} = 9\)
\(N_{\text{females}} = 12 \text{ and } N_{\text{males}} = 8\)
\(N_{\text{females}} = 13 \text{ and } N_{\text{males}} = 7\)
\(N_{\text{females}} = 14 \text{ and } N_{\text{males}} = 6\)
\(N_{\text{females}} = 15 \text{ and } N_{\text{males}} = 5\)
\(N_{\text{females}} = 16 \text{ and } N_{\text{males}} = 4\)
\(N_{\text{females}} = 17 \text{ and } N_{\text{males}} = 3\)
\(N_{\text{females}} = 18 \text{ and } N_{\text{males}} = 2\)
\(N_{\text{females}} = 19 \text{ and } N_{\text{males}} = 1\)
\(N_{\text{females}} = 20 \text{ and } N_{\text{males}} = 0\)

We will look at these for the probability values from 0.1 to 0.9 in steps of 0.1

so the probabilities would be {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9}

Full Code